Exact Straight Line Mechanisms - Peaucellier linkage and Scott-Russell Mechanism
Exact Straight Line Mechanisms
As detailed in the previous articles there are many four bar linkage based mechanisms which can generate straight lines. These mechanisms are simple linkage mechanisms with revolute joints, but they can only generate approximate straight lines and that too only for short lengths. In certain design requirements such as design of production machinery it is desirable to have more accurate straight line paths or sometimes it becomes inevitable to have exact straight line trajectories of mechanisms.
Perfect straight lines can also be generated using a linkage mechanism. When linkage mechanisms are designed to generate exact straight lines the level of complexity increases as compared to the mechanisms designed to generate approximate straight line paths. The first exact straight line generating mechanism was invented by a French army officer Charles Nicolas Peaucellier in 1864. This mechanism is called as Peaucellier Exact Straight Line Mechanism and commonly more as Peaucellier’s linkage. There are many mechanisms based on slider crank linkage which can generate exact straight lines for limited intervals.
Peaucellier Exact Straight Line Mechanism
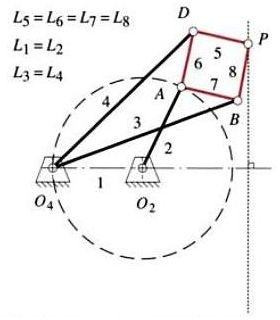
Peaucellier linkage can convert an input circular motion to the exact straight line motion. The construction of this mechanism is such that the point which is connected to the crank moves in a circular path and the point traversing the straight line is selected as the output point. The linkage has a rhombic loop formed of the equal lenght members, 5, 6, 7 and 8. Two equal length length links are connected to the opposite corners of the rhombus at one end and to a common fixed point at the other ends. The point A of the rhombus is connect to fixed point O2 through the link 2. The length of the link 2 is equal to the distance between points O2 and O4. By the constraints of the geometry point A moves in a circular path and as the point A moves in a circle point P traverses an exact straight line path normal to the line joining O2 and O4.
From the construction of the Peaucellier linkage it is clear that this is a much more complex mechanism than the mechanisms generating approximate straight lines, which were simple four bar linkages. This mechanism has eight members and six joints.
Scott-Russell Exact Straight Line Mechanism
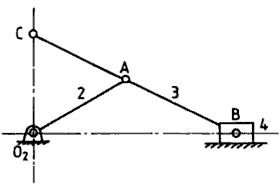
The complexity of the mechanisms to generate exact straight lines can be reduced by introduction of one or more slider crank linkages. It is possible to generate an exact straight line using the slider crank mechanism but the range of motion is limited. One such example is Scott-Russell Mechanism as shown in the figure. Based on the geometry of the linkage the output motion is a simple sine function of the drive link or a simple harmonic motion. It is evident from the figure that this mechanism is made up of isosceles triangles, AB, AC and AO2 are of equal lengths.
This post is part of the series: Kinematics - Design of Mechanisms
Machines as simple as livers, machines such as James Watt’s steam engine and the industrial robots such as PUMA all are composed of mechanisms whether simple, complex or combination of many simple and complex mechanisms. These mechanisms are governed by Kinematics – the study of geometry and motion.
- Kinematics - Design of Mechanisms: Introduction
- Analysis and Synthesis in Machine Design
- Types of Kinematic Joints
- Degrees of Freedom
- Kinematics – Design of Mechanisms: Kinematic Inversion
- Kinematics – Actuation of Machines: Part I – Electrical Actuation
- Kinematics – Actuation of Machines: Part II – Hydraulic Actuation
- Kinematics – Actuation of Machines: Part III – Pneumatic Actuation
- Kinematics - Analysis of Mechanisms: Methods and Techniques
- Kinematics - Synthesis of Mechanisms: Methods and Techniques
- Four Bar Linkages in Machine Design
- Straight Line Mechanisms
- Kinematics - Special Mechanisms: Straight Line Mechanisms - II
- Exact Straight Line Mechanisms