Use the Pipe Flow Reynolds Number for Turbulent Flow to find the Entrance Length for Fully Developed Flow

Categories : Hydraulics in civil engineering
Tags : Civil engineering

Introduction

Equations for analyzing pipe flow, such as the Darcy Weisbach equation for frictional head loss, often apply only to the fully developed flow portion of the pipe flow. If the total pipe length is large compared to the entrance length, then the effect of the entrance length can usually be neglected and the total pipe length can be used in calculations. If the total pipe length is relatively short in comparison with the entrance length, however, then the entrance region may need to be analyzed separately. An estimate of the entrance length is sometimes needed in order to determine how to proceed with pipe flow calculations. The Reynolds number for pipe flow is needed to calculate the entrance length for turbulent flow or for laminar flow.

The Entrance Region

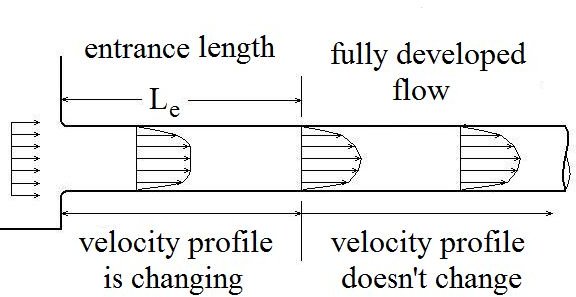
The diagram at the left illustrates the meanings of “entrance region” and “fully developed flow.” When fluid enters a pipe its velocity will often be uniform across the pipe cross-section as shown in the diagram. Near the entrance, the fluid in the center of the pipe isn’t affected by the friction between fluid and pipe walls, but as the flow proceeds down the pipe, the effect of the wall friction moves in toward the pipe center, until the pattern of velocity variation across the pipe (called the velocity profile) becomes constant. The entrance portion of the pipe, where the velocity profile is changing is called the entrance region, and the flow after that entrance region is called “fully developed flow.” The next two sections will present equations for estimating the length of the entrance region, called the entrance length, for pipe flow.

Estimating the Entrance Length

The entrance length for pipe flow is a function of Reynolds number for both turbulent flow and laminar flow. You probably recall that turbulent flow will occur for flow in a pipe or duct if the Reynolds Number (Re) is greater than 4000. Most pipe flow of gases and liquids with a viscosity similar to water is turbulent flow.

For turbulent flow the entrance length, Le, can be estimated from the equation: Le/D = 4.4Re1/6.

where Re = DVρ/μ for flow in circular pipes and Re = 4RHVρ/μ for flow in non-circular ducts, and

D = pipe diameter, ft

V = average flow velocity in pipe (= Q/A), ft/sec

ρ = fluid density, slugs/ft3

μ = fluid viscosity, lb-sec/ft2

RH = hydraulic radius, ft, where RH = A/P, and

A = cross-sectional area normal to flow, ft2

P = wetted perimeter of pipe or duct cross-section, ft

Laminar flow in pipes and ducts takes place for Reynolds Number less than 2100, with Reynolds Number as defined just above. Laminar flow in pipes will occur only for very viscous fluids and/or very slow flows.

For Laminar Flow, the entrance length, Le, can be estimated from the equation: Le/D = 0.06 Re.

Calculation of Typical Entrance Length

Consider flow of 1.2 cfs of water at 50o F through a 4" diameter pipe. What would the entrance length be for this flow?

Solution: The density and viscosity of water at 50oF are: ρ = 1.94 slugs/ft3 and μ = 2.34 x 10-5.

The velocity, V, can be calculated from V = Q/A = 1.2/(πD2/4) = 1.2/[π(1/3)2/4] = 13.4 ft/sec.

Substituting values into Re = DVρ/μ, gives: Re = (1/3)(13.4)(1.94)/(2.34 x 10-5) = 3.79 x 105.

The value of Reynolds number is greater than 4000, so this is turbulent flow, and the entrance length can be estimated from the equation: Le/D = 4.4 Re1/6.

Thus: Le/(1/3) = 4.4[(3.79 x 104)1/6], Le/(1/3) = 37.4, and Le = 12.5 ft.

This post is part of the series: Pipe Flow Calculations

Pipe flow calculations include using Reynolds number to find if the flow is laminar flow or turbulent flow. Frictional head loss can be found using the Darcy Weisbach equation and the friction factor. The entrance length for fully developed flow can be found for turbulent flow and for laminar flow.