How to Use a Smith Chart: Explanation & Smith Chart Tutorial
What is the Smith Chart?
The Smith Chart is the graphical representation of a complex mathematical equation. It is the circular plot of the characteristics of microwave components. The Smith Chart is the most used tool for microwave engineers to visualize complex-valued quantities and calculate the mapping between them. It consists of two sets of circles for plotting various parameters of mismatched transmission lines. One is the set of complete circles whose centers lie on the straight line and the other one is the set of two arc circles which lie on the either sides of the straight line.
The figure to the right shows the Smith Chart. The horizontal axis represents the normalized resistance and the normalized line reactance is shown on the outer edge of the circles. The complete circle of the Smith Chart represents a half wavelength along the straight line.
Applications of Smith Chart
The important applications of a Smith Chart are as follows:
- Admittance calculations on any transmission line, on any load.
- Impedance calculations on any transmission line, on any load.
- Calculation of the length of a short circuited piece of transmission line to provide a required capacitive or inductive reactance.
- Impedance matching.
Before plotting on a Smith Chart we need to study a few terms such as transmission line, characteristic impedance, standing wave, etc.
Transmission Line Theory
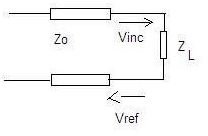
Transmission lines are the circuits that deliver power from a transmitter to an antenna and from an antenna to a receiver. These are the impedance matching circuits. While transferring the RF waves on a finite transmission line, for maximum power transfer from source to load (i.e. transmitter to antenna or antenna to receiver), the impedance of source must be equal to the impedance of load. This is known as impedance matching. If there is impedance mismatching, part of the energy in the incident wave is reflected back giving rise to a standing wave. The ratio of the voltage of reflected wave and the voltage of incident wave is known as the reflection coefficient. It is denoted by Γ.
It is expressed as Γ= Vref / Vinc.
The amount of reflected wave depends upon the mismatching of the source and load impedances. Therefore, from the fig., gamma can be expressed as,
Γ = (ZL - Zo) / ( ZL + Zo ) where, ZL is load impedance and Zo is the characteristic impedance of transmission line, a constant.
ZL= RL + jXL.
Normalized impedance is used for plotting on Smith chart. This is because the behavior of the transmission line depends on load impedance as well as characteristic impedance.
Normalized impedance, Z = ZL/ Zo = r+ jx, where r = R / Z0 and x = X / Z0.
Therefore, Reflection coefficient can expressed as
Γ = (Z-1) / (Z+1) or
Γ = (ZL-1) / (ZL+1) as Zo takes constant values such as 50Ω, 100Ω, etc.
Γ = [(r +jx) - 1] / [(r + jx) + 1]
Γ = [(r - 1) + jx] / [(r + 1) + jx] for r lies between 0 and ∞ , x lies between -∞ and +∞.
The above equation can also be written as
Γ = u + jv = Rejθ , where R is the radius and θ is the angle of incidence.
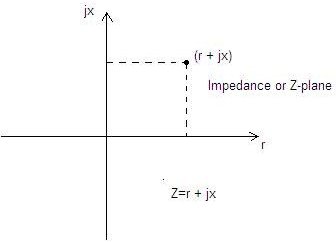
Z = r + jx
From the last two equation, we can see that there is one-to-one correspondence and for every Z we can obtain a unique Γ. Following fig. shows mapping of Z to Γ- plane.
Mapping of Z to Γ- plane
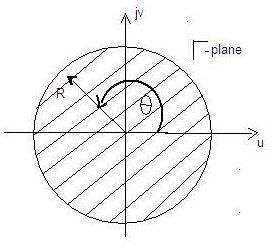
lΓl ≤ 1. Therefore, the possible values of Γ will remain within the unit circle.
Z = (1 + Γ) / (1 - Γ)
r + jx = [1 + (u + jv)] / [1 - (u + jv)]
Separating the real and imaginary part, we get
r = (1 - u2 - v2) / [(1 - u)2 + v2] and
x = 2v / [(1- u)2 + v2]
Furher simplifying the above two equations, we can re-write them in standard circle equation form as
[u- r/(r+1)]2 + (v - 0)2 = [1/(r+1)]2 with center at [r/(r+1), 0] and radius = 1/(r+1) and
(u - 1)2 + (v - 1/x)2 = (1/x)2 with center at (1, 1/x) and radius = 1/x.
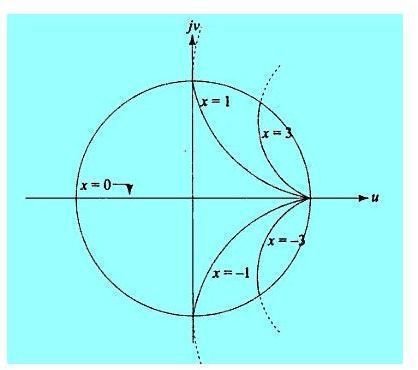
The circles with centers at [r/(r+1), 0] and radii = 1/(r+1) are known as constant resistance circles as shown in following fig.The circles with centers at (1, 1/x) and radii = 1/x are known as constant reactance circles as shown in following fig.
The Smith Chart is drawn by superimposing these two types of circles.
Constant Resistance and Constant Reactance Circles

References
Smith chart image : https://commons.wikimedia.org/wiki/File:Smith_chart_gen.svg
All other images created by author.
References
Electronic Communication Systems By Kennedy and Davis, Tata McGraw Hill, 4th edition.
Electronic Communications By Roddy and Coolen, PHI, 4th edition,
Electromagnetic Waves By R K Shevgaonkar, McGraw Hill.
