The Castigliano Theorem and Ship Design
Introduction
In this article we will discuss the Castigliano’s theorem in relation to the ship design. Now let us discuss how we apply the Castigliano theorem in ship design.
The loads on the transverse section of a ship are calculated from the motions of the ship (which includes gravity forces and the inertia forces along the ship’s length at a given position and the sloshing of the liquids within the tanks. These are the forces that are considered when a ship in a seaway. Additionally the scantlings must be able to withstand the loads due to berthing and racking strains that takes advantage during docking the vessel. Therefore it is necessary to analyse the section of ship between the main transverse bulkheads.
For loads due to berthing it is necessary to isolate a grillage (A group of plating together with their supporting stiffeners in two directions) and to analyse the stresses acting on it. Usually it is a practise to take a section through the ship (which consists of deck beam, side frame, plating and double bottom structure) and then it is loaded and analysed as a framework.
The strength against racking is provided by the transverse bulkhead, some of this support being transmitted to lthe frames that are present remote from the bulkhead by the longitudinal members although these themselves deflects due to loading.
There are different methods for analysis of the frameworks. Some of them are:
1. ENERGY METHOD:
It is based on the Castigliano’s theorem which states that the partial derivative of the total strain energy with respect to each applied load is equal to the displacement of the structure at that point.
2. MOMENT DISTRIBUTION METHOD:
It states that all the members are considered to be fixed. Now the bending moment at the joints are calculated. Now only one joint is relaxed by rotating it. the bending moment is distributed among the members of the framework according to their lengths and inertia. The maximum moment is transmitted to the member which is still fixed (which is member’s far end). Joints are relaxed in turn and repeated until a balance is achieved.
Castigliano’s Theorem
Let us discuss the Castigliano’s theorem in detail:
STATEMENT:
The theorem states that the partial derivative of the total strain energy with respect to each applied load is equal to the displacement of the structure at that point of application of load.
CASTIGLIANO’S THEOREM:
Let us assume the following:
U - Total strain energy,
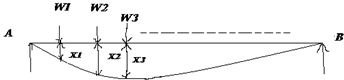
W1, W2, W3,….etc, be the load acting at the points 1, 2, 3, …..
X1, X2, X3,….etc be the displacement at the points 1, 2, 3,…..
Then,
The total Strain energy can be given by:
U= 1/2 W1 X1 + 1/2 W2 X2 + 1/2 W3X3 +…..+1/2 Wn Xn ————————————-(1)
(since Strain energy U = 1/2 X Load X Displacement)
Suppose the load acting at point (1) be increased by a small quantity ∂W1, then,
The increase in the external work done may be written as:
∂U = (W1 + ½∂W1)∂X1 + W2 ∂X2 + W3 ∂X3 +……….
Where,
∂X1 , ∂X2 ,∂X3 ,……… are increases in their displacements respectiveley.
Therefore,
∂U = W1 ∂X1 + W2 ∂X2 + W3 ∂X3 +………. ——————————————————-(2)
(neglecting the small product quantity ½∂X1∂W1)
Therefore, the total strain energy ( if the loads W1 + ∂W1 , W2, W3,…. were applied from zero)
U + ∂U = ½(W1 + ∂W1 )(X1+ ∂X1) + ½W2 (X2+ ∂X2)+……………
Now, subtract the above equation from equation number (1) :
∂U = ½(W1 ∂X1) + ½(∂W1 ∂X1) + ½(W2 ∂X2) + ½(W3 ∂X3) +……. ———————————(3)
(Neglecting the small term ∂W1∂X1)
The above equation may be re-written as
2∂U = (W1 ∂X1) + (∂W1 X1) + (W2 ∂X2) + (W3 ∂X3) +…….
Now, subtract the above equation from equation (2)
∂U = ∂W1 X1
Therefore, the displacement at the point (1) can be given as:
X1 = ∂U / ∂W1
Similarly, we can fine the displacements X2, X3, ………
Note:
- Usually, only Strain energy due to bending need to be taken into account for the deflection of curved beams. (U= ∫ M2 ds/(2EI) )
Where,
M- Moment of Inertia of the section of the beam,
E- Young’s modulus.
Example
Obtain an expression for the vertical displacement at A of the beam as shown:(Assume that the breadth is unit)
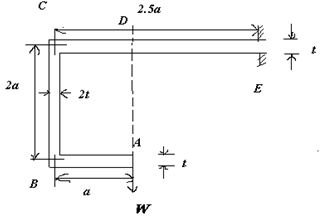
From the sketch, it is clear that “t” is the thickness of the beam, W is the load acting at point A.
The bending moment acting at the section AB shall be written as:
M = W.x ( At x from point A )
The bending moment acting at the section BC shall be written as:
M = W. a ( a constant )
The bending moment acting at the section CD shall be written as:
M= W x'
The bending moment acting at the section DE shall be written as:
M= W x"
Therefore, the total strain energy is
U= ∫ M2 ds/(2EI)
= 0∫a (W2x2)/(2Et3/12) dx + 0∫2a (W2a2)/(2E(2t3)/12) ds + 0∫a (W2x'2)/(2Et3/12) dx’ + 0∫1.5a (W2x"2)/(2Et3/12) dx"
Where I = bd3/12, b = unity, d = t
Therefore the above equation after integration and applying the limits we get
U = 24.5 W2a3/(2Et3)
The displacement of the load at A = ∂U / ∂W ( according to castigliano’s theorem)
A = ∂U / ∂W (24.5 W2a3/(2Et3))Therefore, displacement of the beam is 24.5 Wa3/(Et3)