How does a ship remain stable in the ocean?
Introduction
In this topic we will cover the basic aspects about ship stability starting from the very fundamental concepts which will help you to grasp the subject matter with ease. Since it is vital to understand the concepts behind stability we will start with a discussion of the underlying principles and theories behind the exciting science of ship stability. Such an approach would have the double benefit of being simple to understand for normal readers while it will help you to prepare for your marine certification exams if you are a student in this field.
About Force, Net Force, Moments et al.
I think everyone of us knows the definition of the term “Force” but let me restate it for the benefit of those who have forgotten it. Force can be defined in several contexts for example you may be forced to leave the classroom, or you may be forced to eat your ice-cream but in the context of physics, force can be defined as the something which causes a body to experience push or pull. Technically the value of force is defined as
Force = Mass * Acceleration
The units of force are Newton (units of mass and acceleration are kg and m/s2 respectively), hence it means that if a body of mass 1 kg experiences an acceleration of 1 m/s2 then a force of one Newton is acting on it.
We also know that a vector quantity is one which has got both a magnitude as well as a direction while a scalar quantity is one which has only got magnitude. So can you guess which type of quantity is force? Well if you are confused let me clear that force is a vector quantity since it has a magnitude and direction in which it acts.
Multiple Forces
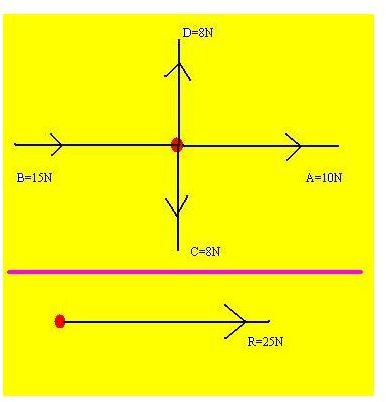
It is quite uncommon that a single force acts on a body and normally there are two or more forces which are acting simultaneously on a body at a given point of time. If the force was a scalar quantity the simple sum of all the forces would have given the net or the resultant force but since it is a vector quantity, the resultant force on the body is the vector sum of the forces acting on it at a time. Let me make this more clear with the help of a diagram shown below in which four forces are acting on a body.
The red coloured dot represents the body and there are four forces acting on it shown by black arrows for direction and magnitude written near them. It can be seen that forces C and D cancel each other (equal but opposite) and force A and B add (same direction), hence the net force on the body will be 25N in the direction of A which is shown below the thick pink coloured line.
Moment of a Force
If you think that moment of a force defines the moment or time period for which the force acts, just wait a moment and read this. Actually the moment of a force defines the turning effect of the force relative to a given point and mathematically it is calculated as the amount of force times the distance between the point of action of the force and the point at which the moment is to be calculated
Ma = F * d
Where M”a” is the moment of the force “F” at a perpendicular distance “d” from the point “a”.
A corollary to the above equation is that when the force acting is due to the weight of an object then the moment is also known as moment of mass.
Multiple Moments
Just like the case of multiple forces described earlier, there could be multiple moments of force or mass relative to a point due to the action of more than one force. In such a case it might be necessary to find the net or resultant moment of force or mass for calculation purposes.
To find the resultant moment relative to a point we first find all moments which tend to have a turning effect in one direction and the moments which tend to have turning effect in the other direction, the directions being clockwise or anticlockwise. The net moment is the difference between these two and the resultant direction is the direction of the moments which are greater in magnitude.
Example
It is best to understand this with the help of an example suppose there is a see-saw and two people are sitting on it as shown in figure below.
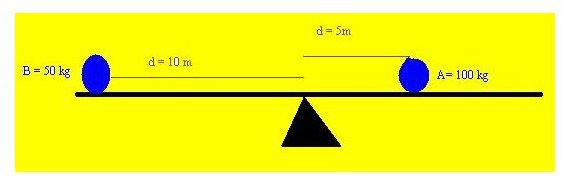
The heavier man is seated at 5 meters distance from the center or fulcrum while the lighter man is at a distance of 10 meters.
Turning moment of body A about the fulcrum = 100 * 5 = 500 kg-m (clockwise)
Turning moment of body B about the fulcrum = 50 * 10 = 500 kg-m (anticlockwise)
Hence the net moment is 500 – 500 = zero kg-m
In the next article we will study about the center of gravity of a body and its application to ship stability.