Metacentric Height and Stability - Why Ships Tend to Stay Upright

Floating bodies normally involve or are associated with tilting capabilities or tendencies. The tilt that may arise about any given axis through minimum inertia is identified as the metacentric height (MH) of the body.

For example suppose if a floating body is forced to tilt by an externally applied force through some minor angle, then the produced point of intersection CB vertically through the new center of buoyancy B, may be termed its metacentre.

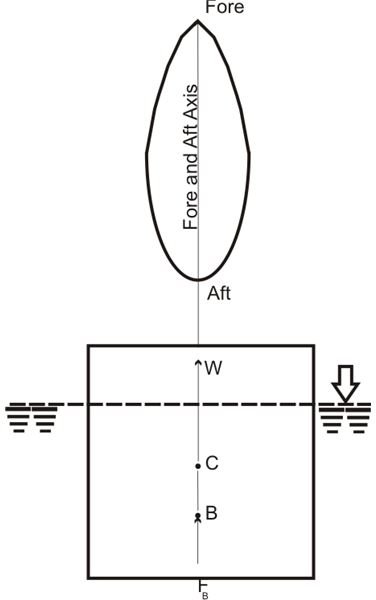
Basically a floating body can be expected to be in either of the following three equilibrium conditions: stable, neutral, or unstable. Referring to the figure on the left, we can see that the above states of equilibrium correspond to M below C, M above C, and M over C or coinciding to C respectively. The length of CM measured from C to M becomes the MH.

In order to sustain stability, the MH of any floating body must be positive. That simply implies that greater the positivity of the metacentric height of a body, the greater stability it is able to attain.

Also, the stable state of a floating body implicates minimum potential energy that may be associated with the body in that state and is the general conclusion adopted in the study of mechanics. Another factor that necessitates the above conclusion is that here the center of gravity should be as minimum as possible.

Calculating Clues

Referring to the figure below, consider a body floating about its fore-and-aft axis with a planeform symmetry. The upright position of the body keeps it in an equilibrium state due to the effect of two equal and opposite forces: its own weight W passing through its center of gravity and the force of buoyancy FB passing through its center of buoyancy.

The force of buoyancy FB is given by:

FB = ρgV

Where ρ is the density and V is the volume of the liquid displaced.

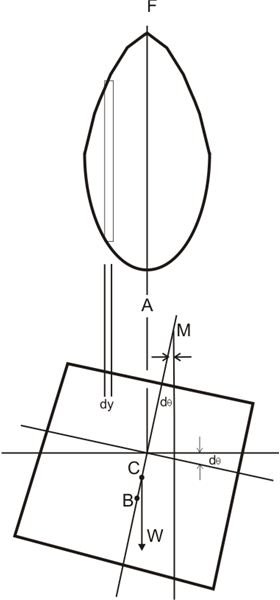
Now suppose as illustrated in the adjoining figure, if the body is tilted about its fore-and-aft axis, this forces the body to go through an unsymmetrical submergence, shifting its center of buoyancy from B to B1.

The metacenter M in the above condition is located by drawing a vertical line BC through B1.

In case of smaller tilt angles,

BB1 = BM.d__θ

Also, at a distance y from the fore-and-aft axis, a small portion of the volume of the liquid dx.dy.yd__θ exerts a moment about the axis due to its weight _dx.dy.yd__θ._ρg which may be expressed as:

dM = dx.dy.yd_._ρ__g.y

Therefore the total moment by the contained liquid in the volume of the shown container over the whole body can be given as:

ρ__g__θ ∫(+y to -y) ∫(F to A) y2dxdy = ρgdθ A∫Fy2dA = ρgdθ/I

However since the above moment must happen about the horizontal shift and also should be equal to it, the force of buoyancy can be written as:

FB.BB1 = ρgdθ.I

ρgV.BM.dθ = ρgdθ.I

Cancelling the common members ρgdθ.I from both sides, we get:

BM = I/V

Where V is the volume of liquid displaced by the body and I is the moment of inertia about the fore-and-aft axis.

Finally the metacentric height of the floating body may be expressed as:

CM = BM – BC = I/V – BC

References

Book: Engineering Fluid Mechanics By K.L. Kumar,

Tha Stability of Floating Bodies - codecogs.com

Fluid Statics - nptel.iitm.ac.in