Understanding Realization of D flip flops from JK Flip-flop and T flip-flop

Introduction

In the previous articles we have already discussed about the conversion of SR flip-flop into a JK flip-flop and converting an RS flip-flop into T flip-flop. In this article let us go about understanding D flip flops and their conversion from T and JK flip-flops.

JK Flip-flop to D flip-flop

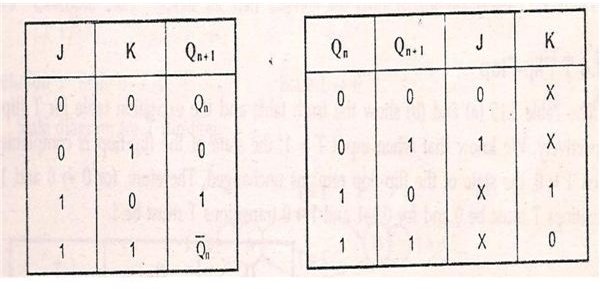
We know that the JK flip-flop has four different transitions from the present state to next state. The four transitions are 0 to 0 transition, 0 to 1 transition, 1 to 0 transition and 1 to 1 transition.

0 to 0 transition occurs when J=0 and K=X.

Where X represents don’t care condition. In other words the value of K may be either 1 or 0 and it will not affect the state of the system.

0 to 1 transition occurs when J=1 and K=X.

1 to 0 transition occurs when J=X and K=1.

1 to 1 transition occurs when J=X and K=0.

From the truth table of D flip-flop it is evident that, the value of next state depends on the D input. In simple words the value of D input is retained for the next state of the system.

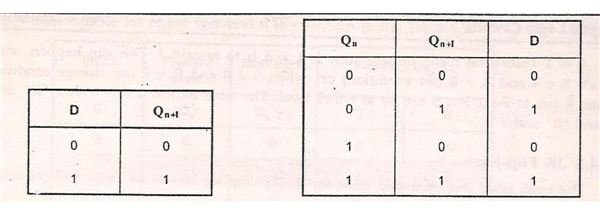
Now from the truth table, we can form the excitation table for D flip-flop. When 0 to 0 transitions occurs, the value of D is 0. When 0 to 1 transition occurs, the value of D is 1. When 1 to 0 transitions occur, the value of D is 0 and when 1 to 1 transition occurs, the value of D is 1.

Now from the JK excitation table and D excitation table, we can deduce the excitation table for the conversion of JK flip-flop to D flip-flop.

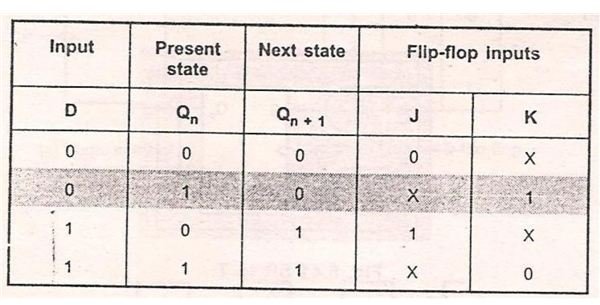
0-> 0 transitions: For 0 to 0 transitions to occur, the value of D input should be 0 and the value of J and K inputs should be J=0 and K=X.

0-> 1 Transition: For 0 to 1 transition to occur, the input for D flip-flop should be D=1 and for JK inputs J=1 and K=X.

1->0 transition: For 1 to 0 transition to take place, the D input should be equal to D=0 and J=X and K=1.

1->1 transition: For 1 to 1 transition to take place, D=1 and J=X and K=0.

From the above excitation table draw 2 separate K-map for J and K inputs respectively, with D and Q (n) as the parameters. Q (n) is the present state of the flip-flop.

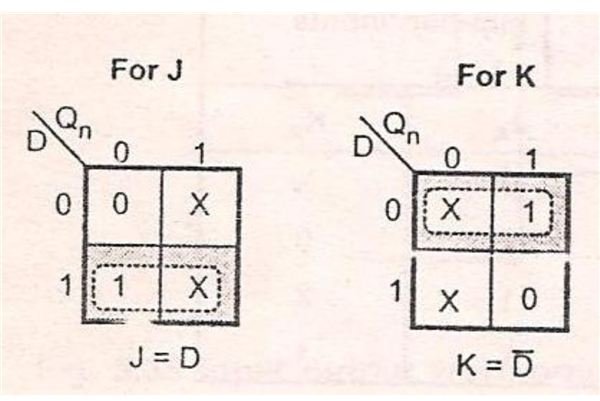
When D=0 and Q (n) =0 the value of J is 0 and the value of K is X. Similarly complete the K-map for different values of T and Q (n).

From the K-map we can deduce two characteristic equations

J=D, where Q’ (n) is the complement of present state Q (n)

K=D’, where Q (n) is the present state of the system.

From this characteristic equation we can draw the logic diagram for the conversion of JK flip-flop into D flip-flop.

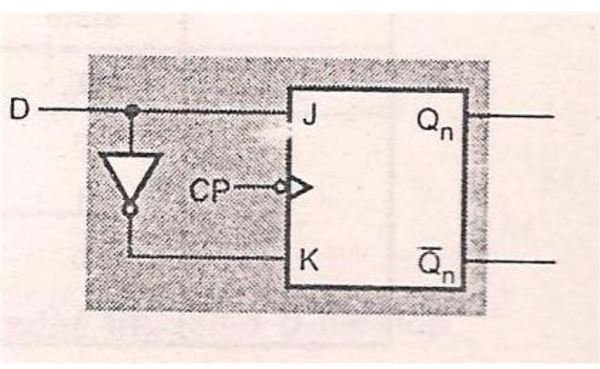
From logic diagram we can see that two NOT gates are used along with J and K inputs to form the D input. Thus the conversion of JK flip-flop into D flip-flop takes place.

T Flip-flop to D flip-flop

Both T flip-flop and D flip-flop has only 1 input each, T and D.

From T flip-flop truth table, we know that when T input is 0, the present state is retained for next state of the flip-flop. When T input is 1, the present state is complemented to get the next state of the system.

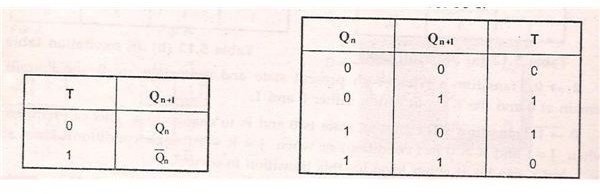
From the T-excitation table and D excitation table, we can form a new excitation table for the conversion of T flip-flop to D flip-flop.

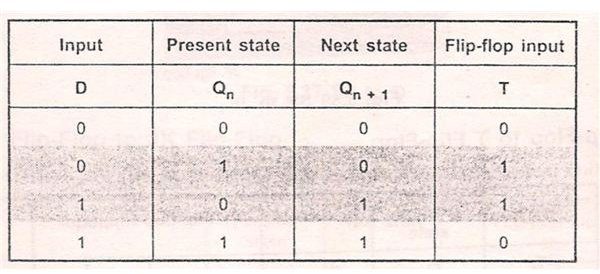
When 0 to 0 transition takes place, T=0 and D=0.

When 0 to 1 transition takes place, T=1 and D=1.

When 1 to 0 transitions takes place, the value of T input is 1 and the value of D input is 0.

When 1 to 1 transition takes place the, the value of T input is 0 and D input is 1.

From the excitation table, we can form a K-map for T input with D and Q (n) as parameters.

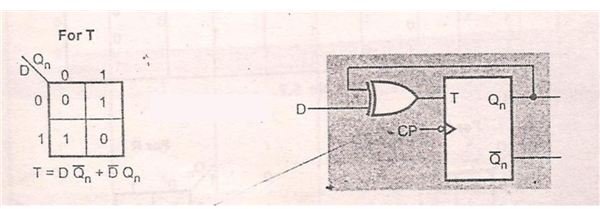
From the K-Map, we can form the characteristic equation. The characteristic equation is

T=D’. Q (n) +D. Q’ (n)

Where D’ represents complement of D and Q’ (n) represents complement of Q (n).

From the K-map we can form the Logic diagram and it satisfactorily explains the characteristic equation.

Thus we have successfully discussed all the important flip-flop conversions.