How to solve electron configurations - Role of Pauli's principle
Introduction
We studied about the four quantum numbers in relation to Bohr’s atomic model in our previous article. In this article we will see the actual electron configuration of some sample atoms and also learn about an important principle regarding these numbers.
Distribution of Electrons
It is all very well to know about various shells, sub-shells and quantum numbers but how do the electrons distribute themselves in light of the concepts in an actual atom. Let us take the example of a Sodium atom and see how this works. As you know the atomic number of sodium is 11, which means that it contains 11 electrons.
So how are these electrons distributed in the atom?
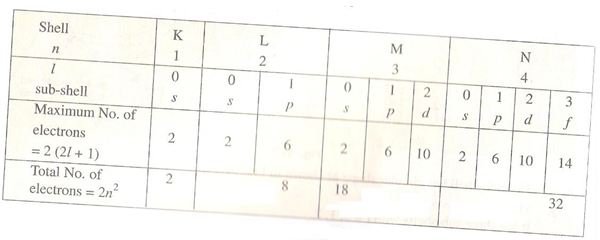
Shell K – this has the value of n = 1, has no sub-shell so the number of electrons in this shell is 2, which are both present in the sub-shell “s”. This is represented as 1s2.
Shell L - this has the value of n = 2, has two sub-shells so the number of electrons in this shell is 8 out of which 2 are in s sub-shell and 6 in p sub-shell. This is represented as 2s2 & 2p6.
Shell M - this has the value of n = 3, has three sub-shells so the number of electrons in this shell is 18 out of which 2 are in s sub-shell, 6 in p sub-shell and 10 in d sub-shell. This is represented as 3s1.
You will notice that the last shell M contains only one electron as rest of the electrons are adjusted in the lower shells. So the overall electron configuration for Sodium in its normal state can be represented in totality as follows.
1s2, 2s2, 2p6, 3s1
Pauli’s Exclusion Principle
After studying the electronic configuration it is not time to take a look at a very important concept known as Pauli’s exclusion principle and stated in simple terms, it states that within an atom, all electrons have unique set of quantum numbers. This means to say that all the four quantum numbers of an atom cannot match in totality with any other electron within the same atom. Of course there can be a maximum match of 3 quantum numbers at the most, but never all four will be the same.
Infact the total number of electrons is a particular shell (as discussed in above section also) can be deduced from this principle and that is why the maximum number of electrons in the shells have their upper limit fixed. Say for example the K shell cannot have more than 2 electrons, while N shell can have max of 32 electrons and so forth. This principle has been verified by experimental results as well. Let us see an simple actual deduction pertaining to the L shell as follows.
We know that for the L shell n = 2.
So the corresponding values of l are 0 and 1
For l = 0 sub-shell, we have only one sub-shell and hence one orbital magnetic quantum number and two spin quantum numbers. This means that if there are more than two electrons the Pauli’s principle will be violated, hence the maximum number of electrons in first sub-shell of L is 2. Similarly it can be reasoned that the maximum number of electrons in second sub-shell is 6.
This means that the total number of electrons in L shell is 8. For your convenience I have given the detailed breakdown of various shells, sub-shells and electron numbers in a tabular format below so that you can check at a single glance.
After having studied the basics of quantum numbers and energy bands, we will now proceed to study about types of bands which would ultimately lead us to the study of semiconductors which form the basis of digital electronics.