Calculating Moment of Inertia Using Routh's Rule and Through the Method of Integration
Moment of inertia is also termed second moment of force or “moment of moment of force.” The term can be understood by first learning the definition of moment of force.
Considering a force “x” about a point, moment of force may be defined as the product of the force and the distance measured perpendicularly between the point of action and the line of action of the force = P.x
The above moment is called the first moment of force.
If the perpendicular distance between the line of action and the point of action is again multiplied by the above moment, then we get what is known as the moment of inertia = P.x2
The moment of inertia of a mass of a body (with area) can be calculated by using either of the two methods:
-
With Routh’s Rule
-
With the Integration Method
Calculating Moment of Inertia Using Routh’s Rule
Routh’s Rule states that if a body is symmetrically shaped about all its three axes, then the moment of inertia about any of its three axes which passes through the center of gravity of the body can be written as:
I = {A (or M) × S} / 3 (for bodies square in shape or rectangular lamina),
I = {A (or M) × S} / 4 (for laminas having circular or rectangular shapes),
I = {A (or M) × S} / 5 (for bodies which are spherical in shape).
Where A = Area of the body
M = Mass of the body,
And S = Sum of the squares of the couple of semi axes, barring the one about which the moment of inertia is being calculated.
Calculating Moment of Inertia Through the Method of Integration
Referring the figure, we see a flat surface whose moment of inertia is needed to be calculated about its X-X and Y-Y axis.
The area is divided into a number of narrow strips and one of the lengths is considered for the calculations.
Let,
dA = The area of the above strip
x = Distance of the center of gravity of the strip over the X-X axis and,
y = Distance of the center of gravity of the strip over the Y-Y axis.
Now, the moment of inertia as discussed in the previous section for the above strip about the Y-Y axis is = dA × x2.
To find the moment of inertia of the entire section, we integrate the above expression and get,
Iyy = ΣdAx2, Ixx = ΣdAy2 and Izz = ΣdAz2
Calculating Moment of Inertia of a Uniform Thin Rod
Two conditions may be considered with this:
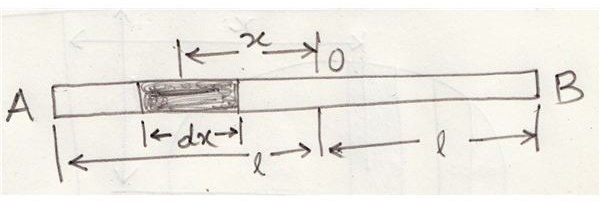
Moment of Inertia about the central axis, at right angles to the length of the rod:
Looking at the figure, consider the rod AB with O as its mid point and length 2l.
Let the total mass of the rod be equal to M and m the mass per unit length of the rod.
We discussed regarding the expression of moment of inertia in the first section, applying it to a small section dx of the rod, at a distance x from the mid point O, we have it as = Mass × x2 = (m.dx)x2 dx
For calculating the moment of inertia of the entire rod, we integrate the above expression across the whole length, i.e. through -l to +l,
Therefore Iyy = ʃmx2dx = m[x3/3] = 2/3ml3,
Since the total mass of the rod is shown as M, replacing 2ml by M, we get,
Ixy = Ml2/3
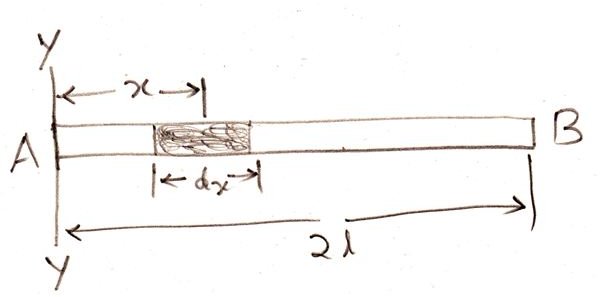
Moment of inertia about the end of the rod, and at right angles to its length.
Referring to the figure we see a rod AB having a length 2l with m as its mass per unit length.
From the above discussions we know that for the shown small section dx of the rod, which is at a distance x from A, about Y-Y axis, its moment of inertia can be written as = Mass × x2 = mdx × x2 = mx2.dx
As done for the previous expressions, the moment of inertia of the whole rod is measured through integration of the above equation across 0 and 2l.
Therefore, Iyy = ʃ mx2.dx = m[x3/3] = m(8l3/3).
Because, the total mass of the rod is equal to M, we can write the above equation as,
Iyy = 4Ml2/3
Units of Moment of Inertia
The units of moment of inertia of a body may be identified from the units of its mass or area or length, we learn them below:
-
The moment of inertia of a body may be expressed in kg.m2, if its mass and distance are in kg and meters respectively.
-
The moment of inertia of an area of a body may be expressed in m4, if its area and distance are in square meters and meters respectively.
-
In case the area is in square centimeters and the distance is in centimeters, the moment of inertia must be given in cm4.
References
- Drawings by author
- Ruth W. Chabay and Bruce A. Sherwood - Matter and Interaction
- Narinder Kumar - Comprehensive Physics XI
