Explanation of How to Solve Inelastic Collision Problems
Elastic vs Inelastic Collision - Types of Inelastic Collisions
During an elastic collision, the momentum and the kinetic energy of an isolated system are conserved. During an inelastic collision however, the momentum and the total energy of the isolated system are conserved. In inelastic collisions, a part of the original kinetic energy is converted to some other form of energy or heat after the collision has taken place but the total amount of energy is conserved.
Inelastic collisions can be classified as half-elastic when the bodies of the system become separated from each other, e.g. during an explosion, and plastic when the bodies of the system do not separate after the collision, e.g. a bullet that remains embedded after hitting a small target.
The article describes the steps on how to solve inelastic and plastic collision problems. In case you are interested to learn more on how to solve elastic collision problems, check out the article, How to Solve Elastic Collision Problems.
Mathematical Background - Energy and Momentum Conservation Principles
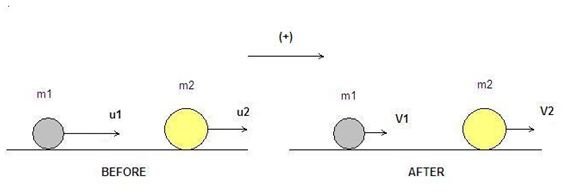
The use of conservation laws in inelastic collision theory is a useful tool for solving these problems. Lets assume that we have a system of two ideal particles with masses m1 and m2 moving in two dimensions. No external forces are acting on the system (closed) and the two masses have initial velocities u1 and u2, respectively. After the collision, their velocities will be V1 and V2, respectively (see image below). Bold letters denote vectors.
According to the conservation of momentum principle, the momentum pBEFORE before the collision is equal to the momentum pAFTER after the collision:
p BEFORE = p AFTER =>
p 1,BEFORE + p 2,BEFORE = p 1,AFTER + p 2,AFTER =>
m1u1 + m2u2 = m1V1 + m2V2
For more information on the conservation of momentum principle, read the article, Understanding the Conservation of the Momentum Principle.
The conservation of kinetic energy K does not apply in the case of inelastic collision. A part of this kinetic energy will be converted to heat or other forms of energy (ΔE). However, the conservation of energy is still valid provided the system is closed:
K BEFORE = K AFTER + ΔE =>
K 1,BEFORE + K 2,BEFORE = K 1,AFTER + K 2,AFTER + ΔΕ=>
(1/2)m1u12 + (1/2)m2u22 = (1/2)m1V12 + (1/2)m2V22 + ΔE
The last expression can be used to calculate the amount of lost energy ΔΕ, when all other parameters are known.
The diagram below shows the general case of an inelastic collision between two objects. In this particular diagram, the velocities of both objects have decreased. (Click to enlarge)
_
Steps to Solve a Plastic Collision Problem
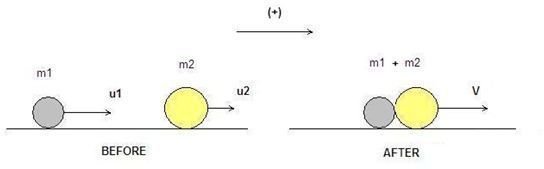
Below are some simple directions that explain how to solve a plastic collision problem in two dimensions_._ Let’s assume that we need to calculate the velocity V of the resulting mass, after the collision has taken place (image below):
- The first step is to design the vectors of velocity for each of the bodies before and after the collision.
- Choose the positive direction, usually toward the right. This helps us to define the sign of velocities ( + or - ) in the equations.
- Write the conservation of momentum. In the case of a plastic collision, the mass of the resulting object is equal to the masses m1 and m2 :
p BEFORE = p AFTER =>
p 1,BEFORE + p 2,BEFORE = p 12,AFTER =>
m1u1 + m2u2 = (m1 + m2)V =>
V = (m1u1 + m2u2)/(m1 +m2)
The result is an expression that calculates the final velocity of the resulting mass.
The diagram below shows plastic collision between two objects. (click to enlarge)
Sources
- Regents Prep - https://www.regentsprep.org/
- Physics247 - https://www.physics247.com/
- Physics.ucsc.edu - https://physics.ucsc.edu/
- Screenshots by author