Themodynamics Boyle's Law
Introduction
Men of Honor is a movie starring Cuba Gooding Jr. and the brilliant Robert De Niro. It is a film based on the life of Carl Brashear, who was not only the first African American to become a US Navy Diver, but was also the first amputee to function as one. There is even a Military Sealift Command Dry Cargo/Ammunition ship, the USNS Carl Brashear , named after this brave man
.
There are two interesting sequences in the film involving Boyle’s Law. In one of them Chief Sunday, who is played by De Niro, sneeringly asks Gooding’s character if he’s ever heard of it. Upon hearing an answer that is of course negative (our hero only had an 7th grade education), Sunday then proceeds to snarl in a tone of utter contempt “Boyle’s Law states that, at a constant temperature, the volume of a confined ideal gas varies inversely with its pressure! Now why is this law important in divin’?”
This law is extremely important in diving because it affects not only the behavior of the deep sea diver as he or she ascends or descends into the depths, but also diving clothing and equipment design.
Boyle’s Law Explained
Boyle’s Law was founded by Robert Boyle (1627-1691), who was one of the great intellectuals of the century. Boyle’s Law in a nutshell states that for a gas, when the pressure is increased, the volume will also decrease. Conversely, if the volume is increased, then the pressure will decrease. Throughout this all, the temperature T is held constant. The volume V is proportional to the pressure P as related in the following equation:
- V ˜ 1/P
or
- P ˜ 1/V
where P is the absolute pressure. Boyle’s Law is normally written as:
- PV = Constant
as well as:
- P1V1 = P2V2
where P1 and V1 are the initial pressure and volume of the gas, and P2 and V2 are its final values.
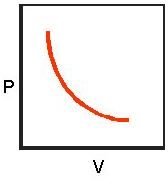
So, for example, if the pressure on a gas is doubled, the volume decreases by one half. You can easily see this from equation 2 if you double the pressure and then solve for P. Figure 2 gives a graphical depiction of this relation.
These results apply for systems where an equilibrium state has been reached, the gas is not too dense, and P is around atmospheric pressure. Because real gases only approximate these conditions, this law is considered to apply to what is known as an ideal gas. Its predictions are accurate enough however, that any gas or gas mixture under proper conditions can meet it. Well-known examples include methane, oxygen, air, and helium.
Now that you know the formula, in part two we will explain the connection between this law and diving.
Image Credits:
Carl Brasher from Chasingthefrog.com
PV Diagram from NASA Glenn Research Center
References
Physics for Scientists & Engineers by Douglas Giancoli
Movie Quotations: ScriptORama.com and MovieTranscriptions.com
Resources
- Wikipedia’s Short Biography
- Stanford’s Comprehensive Biography - includes actual quotations from his writings
- The Coolest Interactive Boyle’s Law Simulation On the Net - it even produces a graph from your data, this is too much!
- A Neat Discussion of the Actual Experiment
