Fluid Velocity Measurement Using a Pitot Tube (Pitot Static Tube)
Introduction
Pitot tubes are used in a variety of applications for measuring fluid velocity. This is a convenient, inexpensive method for measuring velocity at a point in a flowing fluid. Pitot tubes (also called pitot-static tubes) are used, for example, to make airflow measurements in HVAC applications and for aircraft airspeed measurements.
Static Pressure, Stagnation Pressure and Dynamic Pressure - Definitions
Understanding of the terms, static pressure, stagnation pressure and dynamic pressure is very helpful in the explanation of pitot tubes, so they are being defined in this section.
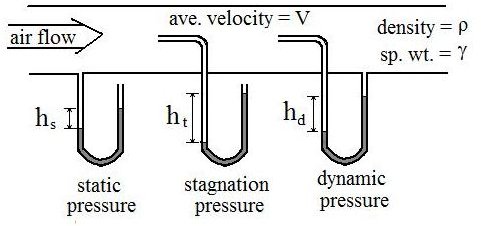
Static pressure is what is commonly called simply the pressure of the fluid. It’s a measure of the amount that fluid pressure exceeds local atmospheric pressure. It is measured through a flat opening that is parallel with the fluid flow. Static pressure measurement is illustrated with the first U-tube manometer in the diagram at the left.
Stagnation pressure is also a measure of the amount that fluid pressure exceeds local atmospheric pressure, but it includes the effect of the fluid velocity converted to pressure. It is measured through a flat opening that is perpendicular to the direction of fluid flow and facing into the fluid flow. Stagnation pressure (also called total pressure) measurement is illustrated with the second U-tube manometer in the diagram at the left.
Dynamic pressure (also called velocity pressure) is a measure of the amount that the stagnation pressure exceeds static pressure at a point in a fluid. It can also be interpreted as the pressure created by reducing the kinetic energy to zero. Its measurement is illustrated with the third U-tube in the diagram at the left.
Static Pressue, Stagnation Pressue and Dynamic Pressure - Relationships
The symbol, P, is often used for static pressure. Dynamic pressure is given by the expression, ½ ρV2. The stagnation pressure is then given by the following equation:
Pstag = P + ½ ρV2 + γh
Where: ρ is the fluid density (slugs/ft3), γ is the specific weight of the fluid (lb/ft3), h is the height above a specified reference plane (ft), V is the average velocity of the fluid (ft/sec). With the specified units for the other parameters, pressure will be in lb/ft2.
Velocity Measurement with a Pitot Tube
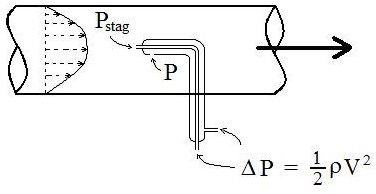
For pitot tube measurements and calculations, the reference plane is taken to be at the height of the pitot tube measurements, so the equation for stagnation pressure becomes:
Pstag = P + ½ ρV2 , which can be rearranged to: V = (2ΔP/ρ)1/2
Where ΔP = Pstag – P.
The pressure difference, Δp, (or Pstag – P), can be measured directly with a pitot tube like the third U-tube in the figure above, or with a pitot tube like that shown in the figure at the right. This is a concentric pitot tube. The inner tube has a stagnation pressure opening (perpendicular to the fluid flow) and the outer tube has a static pressure opening (parallel with the fluid flow).
Example Calculation
Consider a pitot tube being used to measure air velocity in a heating duct. The air is at 85 oF and 16 psia. The pitot tube registers a pressure difference of 0.021 inches of water (Pstag – P). Calculate the velocity of the air at that point in the duct?
Solution: Convert the pressure difference of 0.021 inches of water to lb/ft2 (psf) using the conversion factor, 5.204 psf/in water.
0.021 inches of water = (0.021)(5.204) psf = 0.1093 psf
The density of air at 85oF and 16 psia can be calculated using the ideal gas law, to be 0.002468 slugs/ft3.
(See the article, “Use the Ideal Gas Law to Find the Density of Air at Different Pressures and Temperatures,” for more information.)
Now V can be calculated: V = (2ΔP/ρ)1/2 = [(2)(0.1093)/0.002468] 1/2 = 9.41 ft/sec
Summary
For a fluid with known density and measured difference between stagnation pressure and static pressure (ΔP), as measured with a pitot tube, the fluid velocity can be calculated with the equation: V = (2ΔP/ρ)1/2.