What is Hydrostatic Pressure and Pascal's Law of Pressure in a Static Fluid
Before knowing what hydrostatic pressure is, prior information regarding Pascal’s law would be important, so let’s first learn it.
Pascal’s law states that the pressure at any point inside a static fluid is equal towards all directions in the plane.
The pressure at any point inside a fluid is a magnitude of compressive force or the normal compressive force acting per unit area over that point.
Since there can be an infinite number of planes inside a fluid and hence an infinite number of incidents or normals may be drawn over them at a point, this means (according to Pascal’s law) all these incidents should have an equal distribution of compressive force through them.
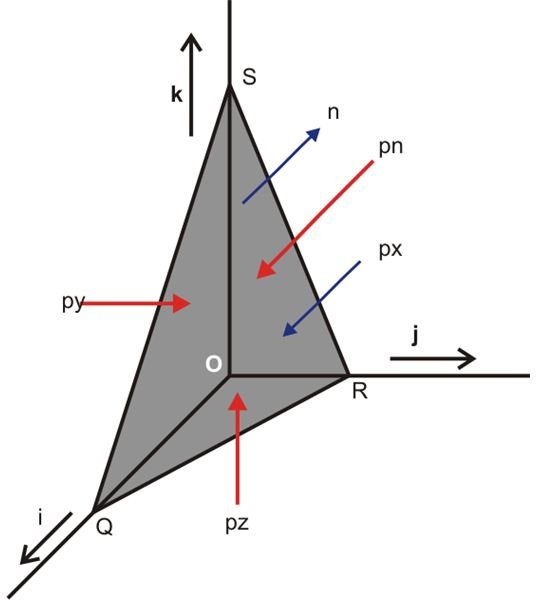
Let’s analyze the fact by taking into account the equilibrium of an infinitesimal small space at a point O (see diagram.)
Pascal’s Law for Static Fluids
As shown in the figure three coordinate axes x, y, and z are arbitrarily selected for the point O.
Consider the point being surrounded by a small tetrahedron OQRS, having three surfaces as ORS, QOS and QRO with areas δAx, δAy and δAz normal to the axes x, y and z respectively.
Also let the pressure on these surfaces be as px, py and pz respectively.
The fourth surface of the tetrahedron which is given as QRS has an area δAn with pressure pn acting normally on it.
Here we won’t consider the weight of the fluid inside the tetrahedron because it’s infinitesimally small and the axes are arbitrarily introduced.
Now, the limits may be represented as,
δAx → 0, δAy → 0, δAz → 0, δAn → 0
The referred pressures px, py, pz and pn are towards the point O.
Now, under the above pressures, for equilibrium of the fluid, the following equations are met:
Ʃ Fx = 0, Ʃ Fy = 0 and Ʃ Fz = 0
Also for the direction x,
px_δAx -_ pn_δAn_ (n.i) = 0,
Where δAn (n.i) is the area of δAn which is shown projected and is normal to the x-axis, can now be represented as δAx.
Therefore the above equation becomes, px_δAX -_ pn_δAx_ = 0
δAx can be cancelled out from both the sides, producing
px = pn
Similarly,
py = pn and pz = pn indicating equilibrium along the directions of the y and the z axes.
Thus finally we can write,
px = py = pz = pn
The above conditions prove that the pressure over all the sides of the tetrahedron or the planes of the enclosed static fluid is equal, confirming Pascal’s law.
Hydrostatic Law of Pressure for Static Fluids
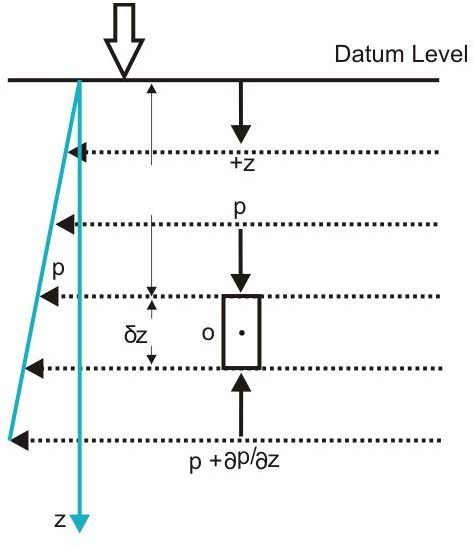
According to the hydrostatic law, at any point inside a static fluid the vertical rate of increase of pressure must equal the local specific weight of the fluid.
The law may be applicable for both compressible and incompressible fluids provided their local density ρ is taken into account. The law is also true for viscous and inviscid fluids as these fluids under static conditions don’t introduce any shearing effect.
As shown in the figure, consider a vertical elementary fluid prism having a cross sectional area a and length δ__z, where it encloses the point O.
In order to assess the above law and understand what hydrostatic pressure is, let’s evaluate the pressure at the point O.
As per the law, for maintaining an equilibrium condition in the z-direction, the sum of all the vertical forces acting at the point O must disappear.
Assume p as the pressure at a depth z below the open surface, the increment in pressure at a vertical depth δz as δp, such that the pressure at a depth δz + z below the open surface is p + δ__p.
Therefore the net resultant pressure exerted upwards becomes:
(p + δp).a – p.a = δp.a,
Also since the gravity force over this prism acts downwards and equals the weight of the enclosed fluid,
Weight = ρg.(δz.a)
Now, to maintain equilibrium,
δpa = ρg.(δz.a),
Therefore, it implies
dp/dz = ρg,
The above expression explains regarding what hydrostatic pressure is and perfectly complies with the stated definition.
Reference (From My Engineering Course)
Author: K.L.Kumar
Book: Engineering Fluid Mechanics (1992)